一维谐振子的相于态|z〉定义为湮灭算符a的本征态，即 a|z〉=z|z〉， 其中z为复数，而湮灭算符a如下给出 其中

一维谐振子的相于态|z〉定义为湮灭算符a的本征态，即

a|z〉=z|z〉，

其中z为复数，而湮灭算符a如下给出

其中，而m、ω分别为谐振子的质量、频率．(1)试求解该相干态的坐标表象波函数；(2)试对该相干态计算Δx·Δp．

一维谐振子的湮灭算符(自然单位)的本征方程表示为a|α〉=a|α〉，|α〉可以表示为谐振子能量本征态的相干叠加，|α〉=．试证明：归一化的本征态|α〉可以表示为

其中|α〉称为谐振子的相干态．

一维谐振子的Hamilton算符为

(1)

x与p满足基本对易式

[x，p]=xp-px=ih (2)

引入无量纲算符

，(3)

(4)

一维谐振子，其能量算符为

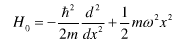(1)

设此谐振子受到微扰作用

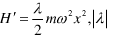(2)

试求各能级的微扰修正(三级近似)，并和精确解比较．

电荷为q的谐振子，t＜0和t＞τ时处于自由振动状态，总能量算符为

(1)

能量本征态记为ψ_n，能级．当0≤t≤τ，外加均匀电场，总能量算符变成

(2)

H的本征态记为φ_n，本征值为E_n．

设t≤0时该谐振子处于基态ψ₀，求t＞τ时的波函数ψ(x，t)，以及ψ(x，t)中各能量本征态ψ_n的成分．

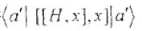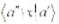设一维粒子的HaniltonianlI,坐标算符为x。利用利用能量木征态的完全性关系，将用和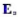，表出，其中是能量本征值为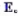，的本征矢。

电子的磁矩(算符)为

试对|ljm_j〉态计算μ_z平均值．

一质量为m，在一维势箱0＜x＜a中运动的粒子，其量子态为

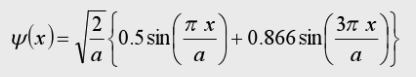
(1)该量子态是否为能量算符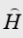的本征态？(2)对该系统进行能量测量，其可能的结果及其所对应的概率为何？(3)处于该量子态粒子能量的平均值为多少？