题目
A.0
B.3
C.2
D.1
 更多“抛物线y=﹣x^2+2x+3与y=2x轴的两交点个数是()个”相关的问题
更多“抛物线y=﹣x^2+2x+3与y=2x轴的两交点个数是()个”相关的问题
第2题
第3题
计算下列第一型曲线积分:
(1)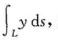 其中L为抛物线y2=2x上点O(0,0)到A(2,2)之间的弧段;
其中L为抛物线y2=2x上点O(0,0)到A(2,2)之间的弧段;
(2)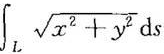 ,其中L为以原点为圆心,a为半径的上半圆周;
,其中L为以原点为圆心,a为半径的上半圆周;
(3)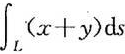 ,其中L为以O(0,0),A(1,0),B(1,1)为顶点的三角形边界;
,其中L为以O(0,0),A(1,0),B(1,1)为顶点的三角形边界;
(4)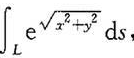 ,其中L为圆周x2+y2=a2,直线y=x及x轴在第一象限内围成的扇形的整个边界;
,其中L为圆周x2+y2=a2,直线y=x及x轴在第一象限内围成的扇形的整个边界;
(5)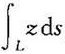 ,其中L为曲线段
,其中L为曲线段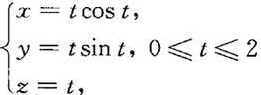 ;
;
(6)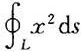 ,为圆周
,为圆周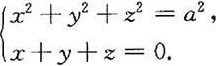
第4题
第8题
A.抛物线开口向上
B.抛物线的对称轴是直线x=1
C.当x=1时,y的最大值为-4
D.抛物线与x轴的交点坐标为
第9题
求抛物线y=x2与直线x=1,y=0所围平面图形分别绕x轴与y轴旋转一周而成的旋转体的体积。
第10题
第11题
如图所示,一质点沿光滑的抛物线轨道,从起始位置(2,2)无初速地滑下。问质点将在何处离开抛物线?抛物线方程为y^2=2x,式中x、y以m为单位。


 警告:系统检测到您的账号存在安全风险
警告:系统检测到您的账号存在安全风险
为了保护您的账号安全,请在“赏学吧”公众号进行验证,点击“官网服务”-“账号验证”后输入验证码“”完成验证,验证成功后方可继续查看答案!
