验证下列（1)、（2)等式，并与（3)、（4)两式相比较： （1)∫f（x)dx=f（x)+C； （2)∫df（x)=f（x)+C； （

验证下列等式,并与(3)、(4)两式相比照:

(1)

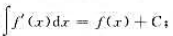
(2)

((3)、(4)两式见教材)

验证下列(1)、(2)等式，并与(3)、(4)两式相比较： (1)∫f(x)dx=f(x)+C； (2)∫df(x)=f(x)+C； (3)[∫f(x)dx]=f(x)； (4)d∫f(x)dx=f(x)dx。

证明下列集合论中的等式：

(1)A∩A=A； (2)A∪A=A；

(3)； (4)；

(5)； (6)

A.4

B.3

C.2

D.1

观察下列等式：1×2=13(1×2×3－0×1×2），2×3=13(2×3×4－1×2×3），3×4=13(3×4×5－2×3×4），4×5=13(4×5×6－3×4×5），…利用上观察下列等式：1×2= 1 3 (1×2×3-0×1×2 ），2×3= 1 3 (2×3×4-1×2×3 ），3×4= 1 3 (3×4×5-2×3×4 ），4×5= 1 3 (4×5×6-3×4×5 ），…利用上述等式，直接写出结果：1×2+2×3+3×4+…+n（）=______．

A.1/(√2+1)⁶

B.(99-70√2)

C.(3-2√2)³

D.1/(3+2√2)³

A.12x = 2y

B.3x^2 — 2 = 2x^2

C.2x^3 — 3 = 3x

D.3x^5 — 7 = 3x — 52x + 110x — 1

A.#图片0$#

B.#图片1$#

C.#图片2$#

D.#图片3$#

设P(B)＞0,事件A和B两足什么关系时,下列等式成立？

(1)P(AIB)=0

(2)

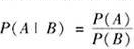
(3)P(AIB)=1

A.x2﹣2x﹣1＝（x﹣1）2

B.x2y2+2xy+1＝（xy+1）2

C.（x+3）（x﹣3）＝x2﹣9

D.8a3﹣2a＝2a（4a2﹣1）

(1) A+BC=(A+B)(A+C)

(2)

(3)

(4)

(5)

(6)