题目
已知氢原子的一个波函数为∮=A(r/a0)2
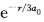 sin2θsin2∮,试求一电子处在该状态时的能量E、角动量|M|以及角动量在磁场方向的分量。
sin2θsin2∮,试求一电子处在该状态时的能量E、角动量|M|以及角动量在磁场方向的分量。
 更多“已知氢原子的一个波函数为∮=A(r/a0)2sin2θsin2∮,试求一电子处在该状态时的能量E、角动量|M|以及角”相关的问题
更多“已知氢原子的一个波函数为∮=A(r/a0)2sin2θsin2∮,试求一电子处在该状态时的能量E、角动量|M|以及角”相关的问题
第1题
已知氢原子的一个波函数为∮=A(r/a0)2
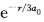 sin2θsin2∮,试求一电子处在该状态时的能量E、角动量|M|以及角动量在磁场方向的分量。
sin2θsin2∮,试求一电子处在该状态时的能量E、角动量|M|以及角动量在磁场方向的分量。
第2题
已知氢原子基态波函数为
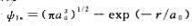
(1)试求氢原子基态的能量和角动量.
(2)求氢原子ψ1.在r=a0和r=2a0处的比值.
第4题
一个氢原子的初始态为
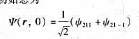
(a)求出含时波函数 (r,t),并尽可能简化表示式.
(r,t),并尽可能简化表示式.
(b)求出势能的期望值(V).(它是否依赖时间t?)给出公式结果和用eV表示的数值结果.
第5题
证明:氢原子2p和3d态径向概率密度的最大值分别位于距核4a0和9a0处。2p和3d态波函数径向部分分别为
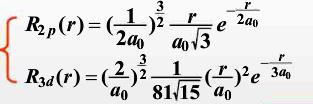
式中,a0为玻尔半径。
第6题
实际原子核不是一个点电荷,它具有一定大小,可近似视为半径为R的均匀分布球体.测量表明,电荷分布半径

试用微扰论估计这种(非点电荷)效应对原子的1s能级的修正(设1s电子波函数近似取为类氢原子的1s态波函数).
第8题
已知氢原子处于由如下波函数描述的状态
其中R21为归一化径向波函数(量子数n=2,l=1).
第10题
已知氢原子的径向波函数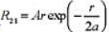 ,其中a为波尔半径。
,其中a为波尔半径。
(1)求归一化常数A。
(2)已知连带勒让德函数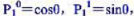 求氢原子的归一化本征函数
求氢原子的归一化本征函数
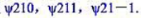
(3)对于本征态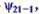 其对应的能量、角动量、角动量z分量各是多少?
其对应的能量、角动量、角动量z分量各是多少?

 警告:系统检测到您的账号存在安全风险
警告:系统检测到您的账号存在安全风险
为了保护您的账号安全,请在“赏学吧”公众号进行验证,点击“官网服务”-“账号验证”后输入验证码“”完成验证,验证成功后方可继续查看答案!
