一个直径为10mm的铜球，初始温度为tI,突然被置于一大气压下饱和水的水浴中，试用集总参数法分析

(2009年)将初始温度为t0的小铜球放入温度为t∞的水槽中，如果用集总参数法来分析，则在经过的时间等于时间常数τr=ρcV／(hA)时，铜球的温度应为()。

A.0．368t∞+0．632t0

B.0．618t∞+0．382t0

C.0．5t∞+0．5t0

D.0．632t∞+0．368t0

一物体其初始温度为T_i，被置于温度T恒定的房间内，由于对流与辐射传热而被冷却．这一传热过程遵从牛顿冷却定律，其中A是物体表面积，h为一常量．已知物体比热容为c，质量为m，试求出物体经时间t后的温度．

面传热系数为24W/(m ²·K)，试计算钢球冷却到300℃所需的时间。已知钢球的c=0.48 kJ/(kg·K),ρ=7753kg/m ³,λ=33 W/(m·K)

加热到6000℃后被分别置于2000的盛有静止水的大容器及200℃的循环水中。用热电偶测得，当因球中心温度从6500℃变化到4500℃时，其降温速串分别为1800℃/s及3600℃/s.试确定两种情况下银球表面与水之间的表面传热系数。已知在上述温度范围内银的物性参数为

已知:一直径为d的钢球加热到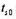温度后，被突然置于温度为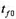的液体中冷却。由于液体的容积有限，在钢球冷却过程中，液体也逐渐升温。为强化钢球表面与液体之间的换热过程，液体槽中加了搅拌器，因而可以近似地认为任一槽间夜槽中的温度是均匀的。表面传热系数为常数。

求:导出确定钢球温度及油温随时间变化的微分方程式，并求解之。

一初始温度为t0的物体，被置于室温为t∞的房间中。物体表面的发射率为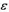,表面与空(间的换热系数为h物体的体集积为V,参数与换热的面积为A,比热容和密度分别为c及。物体的内热阻可忽略不计，试列出物体温度随时间变化的微分方程式。

在一个大气压下，水的饱和温度为（100℃)。

已知:一直径为25mm的金属球壳，其内置有电热器，该球被悬吊于温度为20℃的盛水的容器中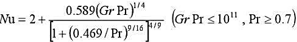，特征长度为球的外径，定性温度为求:为使球体表面温度维持在65℃，电加热功率为多大？

容器中的水在定压下被加热,当最后（)全部变成蒸汽而温度仍为（)温度时,此时的蒸汽称为干饱和蒸汽。

A.未饱和

B.湿饱和

C.干饱和

D.过热