题目
设二阶线性微分方程y+py+qy=f(x)有三个特解y1=ex,y2=ex+ex/2,y3=ex+e-x,求该方程.

 更多“设二阶线性微分方程y+py+qy=f(x)有三个特解y1=ex,y2=ex+ex/2,y3=ex+e-x,求该方程.”相关的问题
更多“设二阶线性微分方程y+py+qy=f(x)有三个特解y1=ex,y2=ex+ex/2,y3=ex+e-x,求该方程.”相关的问题
第1题
设二阶线性微分方程y+py+qy=f(x)有三个特解y1=ex,y2=ex+ex/2,y3=ex+e-x,求该方程.
第2题
设已知二阶线性微分方程
y"+P(x)y'+Q(x)y=f(x)
相应齐次方程两个线性无关的解是y1(x)、y2(x),试用常数变易法,求非齐次方程的一个特解.
第3题
设y1,y2是二阶非齐次线性微分方程y''+P(x)y'+Q(x)y=F(x)的两个解, 则对应齐次方程y''+P(x)y'+Q(x)y=0的解为?
第4题
设二阶非齐次线性微分方程y"+p(x)y'=f(x)有一特解
第5题
设函数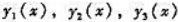 是某二阶线性非齐次微分方程y"+p(x)y'+q(x)y=f(x)
是某二阶线性非齐次微分方程y"+p(x)y'+q(x)y=f(x)
的三个线性无关解[见下面的注①],c1和c2为任意常数,则该徽分方程的通解为().
A.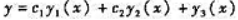
B.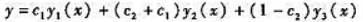
C.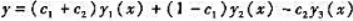
D.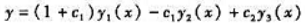
第6题
A.f1(x)·f′2(x)-f2(x)f′1(x)=0
B.f1(x)·f′2(x)-f2(x)·f′1(x)≠0
C.f1(x)f′2(x)+f2(x)·f′1(x)=0
D.f1(x)f′2(x)+f2(x)f′1(x)≠0
第8题
设y1(x)=x,y2(x)=2x-ex是某二阶齐次线性微分方程的解,问C1x+C2ex是否为该方程的通解?
第9题
设y1=x,y2=x+e2x,y3=x(1+e2x)是二阶常系数线性非齐次方程的特解,求该微分方程的通解及该方程.

 警告:系统检测到您的账号存在安全风险
警告:系统检测到您的账号存在安全风险
为了保护您的账号安全,请在“赏学吧”公众号进行验证,点击“官网服务”-“账号验证”后输入验证码“”完成验证,验证成功后方可继续查看答案!
